これを書いていてふと気づいたのですが,構造関係のネタは今のところ全てが骨組み計算モノだったりします.
まぁ,”構造解析とは骨組み計算に始まり骨組み計算に終わる”(?)と思っている程の好き者だったりするので,仕方がないといえば仕方ないのですが.
例えば,軟弱地盤上に構築された橋台が背面盛土により前面側に押し出されるようなケースでは,場合によってはFEMよりも骨組計算の方が簡単に実挙動に近い結果を表現できることがあります.今回は土質と構造のちょうど中間的な話題となりますが,骨組計算による橋台変位の解析方法についてまとめてみました.
このような現象をFEMで解析すると,背面盛土により橋台は全体としては前面に押し出されるのですが,引き込み沈下の影響で,天端部は逆に背面側へ向かう方向に大きく回転変位して,単純に”前に押し出される”形状の変形とはならないことが多いようです.
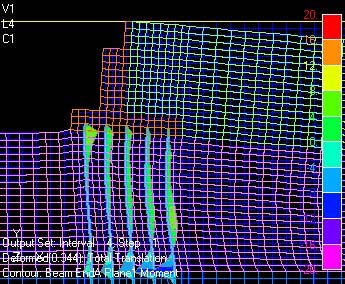
これは,FEM解析では基礎部および橋台の躯体と地盤との間が”ずれ”ないために生じる現象です。
このような現象を避けるために,例えば仮想背面位置などにジョイント要素を設ける手法もあるのですが,ジョイント要素位置での変位があまりにも大きくなり,一般的な条件では収束異常により途中でコケて(力尽きて)しまい,収束判定を甘くするなどの”裏技”が必要となる場合も多いです.
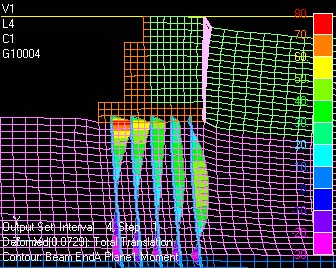
このような解析では,むしろ骨組計算ソフトを使った方が実現象を表現し易いことがあります.
ポイントは,沈下と押し出しによる外力の考え方となります.
まず,沈下による下向きの荷重について.
沈下する地盤が,どれだけの力を橋台に伝えられるか,表現を変えて言えば”ずれ”を生じている両者の間に働くことができるせん断力の最大値について考えてみます.
これを簡単に言ってしまうと,両者の間に作用する土圧に,その面での摩擦係数を乗じた力となります.
設計上の仮想背面は,上図のように橋台の基礎後端より鉛直に立ち上げた面と仮定している場合が多いのですが,基礎後端と躯体天端とを結ぶ斜めの面が実際の土圧の作用面に近いのではないかと思われます.
どちらの面で考えても良いのですが,その仮想背面方向に作用できる最大のせん断力は,土圧合力に仮想背面での摩擦係数を乗じた値となります.荷重の作用位置は普通は基礎後端としますが,仮想背面形状の考え方により,背面盛土による自重と土圧によるせん断力の大きさ,およびその作用方向が変化するので注意が必要となります.
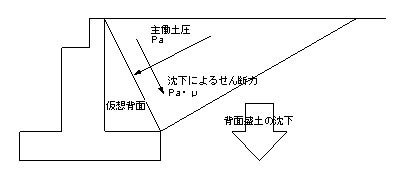
沈下によるせん断力(基礎後端と躯体天端とを結ぶ仮想背面の場合)
次に押し出しによる付加土圧について.
押し出しによって,基礎に作用する水平方向の付加土圧の大きさと形状を正確に決定することは一般に難しいと思います.
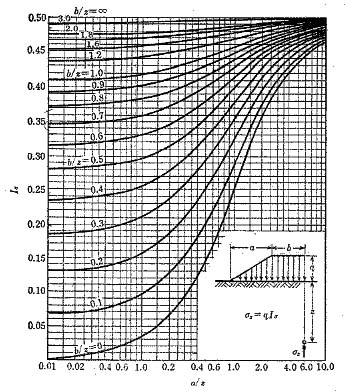
このためあくまでも一つの事例となりますが,例えばフーチング後端より鉛直下向きに想定した一種の仮想背面に対して,背面盛土の形状と大きさからOsterbergの図表に基づき算出した増加応力σzに土圧係数を掛けて水平荷重σxを算出して,これを深さ方向への付加土圧とする方法が考えられます.(他にも長方形分布,中央部が最大となる三角形分布など,色々な分布形状が想定されます)
盛土による瞬間的な(非排水の)変形であることから,ポアソン比は理想的にはν=0.5となり,土圧係数もK=1.0となりますが,現実にはK=0.5〜1.0の範囲となる場合が多いように思われます.
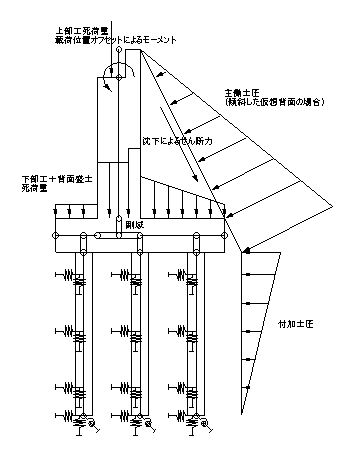
橋台の橋軸直角方向モデルに対して,上部工,下部工の自重,通常の背面土圧に加え,上記の沈下による下向きの荷重,および水平方向の付加土圧を載荷します.なお,付加土圧は後端の杭列への分担が大きくなるよう適当に重み付けをして複数の杭列に載荷します.
なお,現実には杭は飛び々々に存在していますが,杭間隔が2.5Dなどの一般的な配置である場合には,橋台の奥行き方向の全幅の剛性を考慮したモデルに対して,やはり全幅の荷重を載荷するのが妥当ではないかと思われます.
以上の条件に基づき計算を行うと,比較的キレイに水平方向に卓越した押し出し現象を再現することができます.但し,FEMより精度の高い計算をしているという訳ではなく,構造系に対して自由に荷重を載荷できるので,結果的に計算結果を実挙動と合わせ易いというのが実情なので注意が必要です.
また,土圧の分布形状,大きさなど,様々なパターンが想定できるので,結局は逆解析的にパラメータを詰めていく必要があります.
”ずれ”による影響が大きい実現象などを扱う場合には,何が何でもFEMというよりも,むしろこのような解析の方が,はるかに簡単に実挙動に近い結果を再現できることがあります.
勿論,両方の解析を行うことで,各要因の影響の度合いを比較検討することができるので,その方がより望ましいアプローチだと思います.
解析の幅を広げるため,目安としての近似解として,あるいは話のタネとして,骨組計算ソフトにこんな使い方もあることを知っておいて損はないのではないでしょうか.


