N値からの土性値の推定は,地質調査業務の中でごく一般的に行われていることです。
しかし実際の土は,基本的な土性値であっても単純にN値との相関だけでは語り尽くせないケースがほとんどです。ここでは,そのような代表例として,N値とφの関係についてまとめてみました。
現在,ボーリング調査を行う際に標準貫入試験を併用しないことはほとんどない,と言って良いほど標準貫入試験,N値は一般化しています。そして,N値は土の硬軟,締まり具合を示す指標であるため,良かれ悪しかれN値との相関から様々な土性値が推定され,各種の解析や設計に利用されています。
そのようなN値と土性値の相関性を利用している代表的な事例として砂のせん断抵抗角φの推定が挙げられます。
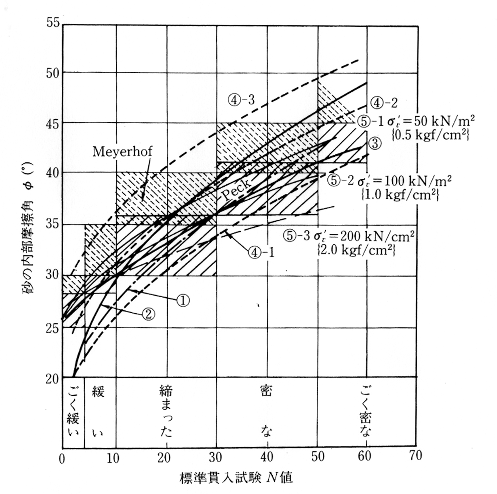
N値とφの関係;「地盤調査法」(地盤工学会)より
砂地盤は,不攪乱試料のサンプリングが難しいので実際にせん断試験を行うことはむしろ稀であり,多くの場合はN値からせん断抵抗角φdが推定されています。そして,砂のN値とせん断抵抗角φdとの相関については,Terzaghi and Peck,Meyerhof,Dunham,大崎らによって多くの提案がなされており,また例えば道路土工などでは次式が提示されています。
φ = √(15*N) + 15 (deg.)
最近では,単純にN値との相関ではなく,有効上載圧σv'をも考慮したタイプの相関式が主流になってきていますが,それでもこれらの式が意味するところを要約すると,次のようになるのではないでしょうか。
仮説1:【N値とφdは相関する】
⇒ つまり同じ材料組成の砂であってもN値の大きい(≒良く締まった≒間隙比の小さい)状態にある砂のφdは,
N値の小さい(≒緩い≒間隙比の大きい)状態にある砂のφdよりも大きい。
これだけを読むと,”当たり前じゃないの?”と思ってしまいそうですが,でもちょっと考えてみてください。これって結構大きな疑問を含んでいませんか?
前述のように,砂地盤はサンプリングが難しいため実際にせん断試験を行うことは稀ですが,それでももし厳密にせん断強度を知る必要がある場合であれば,凍結サンプリングなどにより試料を採取して何らかのせん断試験(一面せん断試験,三軸圧縮試験,など)を行うと思います。
対象とする地盤が砂であることから,例えば三軸圧縮試験(CD条件)を行うとすると,その時の試験手順は概ね次の通りです。
【圧密過程】
同一試料から作成した3個以上の供試体について,それぞれ大きさの異なる等方応力のもとで圧密させる。
【軸圧縮過程】
圧密したそれぞれの供試体について,軸ひずみを与えることで主応力差を生じさせ,せん断破壊させる。
【データの整理】
せん断破壊させたそれぞれの供試体のモールの応力円の包絡線の切片と傾きからcd,φdを求める
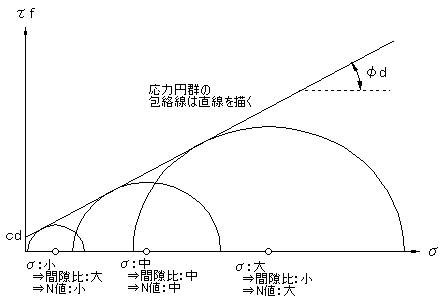
三軸圧縮試験結果の整理例
何が言いたいのかというと,三軸圧縮試験ではそれぞれ大きさの異なる応力で圧密した(⇒間隙比が異なる⇒締まり具合が異なる⇒三段論法的に言えばN値が異なることに相当する)供試体の応力円群を直線で包絡させてcd,φdを求めている,ということです。これを要約すると,次のようになるのではないでしょうか。
仮説2:【材料組成が同じ砂であればφdは同じ】
⇒ つまり同じ材料組成の砂であれば,締まり具合が違ってもせん断抵抗角φdは同じであり,
そもそも,だからこそ異なる圧密圧力の応力円群を直線で包絡することができる。
もう少し説明すると,もし仮説1のようにN値とφdが相関するのであれば,これを単純に表現するとN値が小さい(≒緩い≒圧密圧力が小さい)領域ではφdが小さく,N値が大きい(≒良く締まった≒圧密圧力が大きい)領域ではφdが大きくなるので,これらの包絡線は直線とはならず下に凸な曲線を描くことになりませんか?(下の図はちょっと極端ですが)

N値とφdが相関する場合の包絡線
また,仮説2のように材料組成が同じならφdは同じなのであれば,当然応力の大きさには無関係に包絡線は直線を描くので,この二つの仮説が意味していることは,一見矛盾しているように見えるのですが,どう思いますか?
実は,私もこの問題の正解を完全に理解している訳ではないのですが,次のようなことではないかと考えています。
端的に言ってしまうと,緩い砂と密な砂とではφdは変化します。その意味においては,N値と(間隙比と)φdは相関する,ということになります。但し,これは砂のダイレイタンシーによる”見掛けの”せん断抵抗分をφdに含んでいるからです。
一般に砂をせん断すると,体積が変化します。特に密な砂ほど体積増加(正のダイレイタンシー)が大きくなり,全せん断抵抗力は,本来のせん断変形によるせん断抵抗力に,ダイレイタンシーによるせん断抵抗力を加えた値が計測されることになります。このダイレイタンシーによるせん断抵抗力がφdに及ぼす影響の度合いは一般に無視できない程大きく,密な砂ではφdで10(deg.)近くにも達する場合があります。
なお,このダイレイタンシーによるせん断抵抗力を差し引いて,せん断変形のみによるせん断抵抗力で整理すると,緩い砂でも密な砂でも同じ材料組成の砂であれば,ほぼ同じφdを示すことは良く知られています。
一方,三軸圧縮試験において,このダイレイタンシーによるせん断抵抗力を差し引く処理(エネルギー補正)は一般に行われていないことが多いので,非常に緩い状態から非常に密な状態までの広い応力領域で,多数の供試体を用いてせん断試験を行い包絡線を描くと,恐らく下に凸な曲線を描くものと考えられます。(実際にはもう少し複雑な曲線を描くのでしょう,またここでは他の粒子破砕による影響などは考慮していません)。
では,なぜ一般的なせん断試験では包絡線を直線として描けるのかというと,通常は上述のような現象が顕著に表れるほど大きな(広い)応力領域を対象としていないことが原因の一つではないかと想像してるのですが,あまり自信はありません。また3個程度の応力円では,なんとか直線が引けてしまう(?),ということもあるかも知れません。
この辺は,土質試験を専門にされている方々のご意見や体験等を教えていただきたいところです。
参考までに,Leeらは,強度への寄与因子として,次のような概念図を示しています。
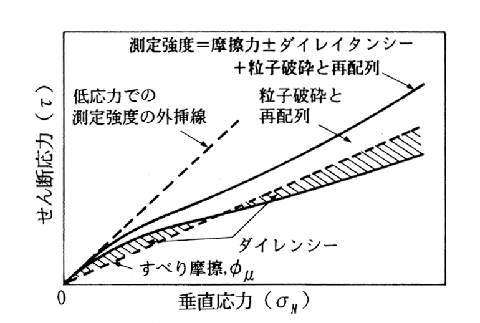
強度への寄与因子の概念図;「N値およびc・φ」(地盤工学会)より
これまた,何とも云いようのない微妙な曲線ですね。σが小さい領域では逆に負のダイレイタンシーの影響を受けるため全体としてはS字曲線となっています。この図を見ると,もっと大きな応力領域では一体どんな曲線を描くのか非常に興味深いものがあります。(やっぱり下に凸なんでしょうか?)
また文献などでは,N値は概ね相対密度の自乗に比例するような曲線を示しているものが多いのですが,圧密圧力,間隙比とN値の相関は今回の問題に大きな関連があるので,機会があれば扱ってみたいテーマの一つです。
”N値から砂質土のφdを推定する”というきわめて日常的・基本的な行為の中にも,このような地盤工学的な問題が存在するということには,”土”の奥深さを感じてしまいます。あと,やっぱりもう少しクリアーに理解する必要があるみたいですね,”勉強が足らん”ということなのでしょう。
関連文献等
「地盤調査法」社団法人地盤工学会
「N値およびc・φ」社団法人地盤工学会
「道路土工 仮設構造物工指針(平成11年3月)」社団法人日本道路協会
太田秀樹:「講座 カムクレイに学ぶ 3.模索−新事実の発見−の時代」土と基礎(1993.8)社団法人地盤工学会


