斜面安定,支持力は,いずれも土のせん断に関する問題です。それなのに斜面安定の安全率は Fs = 1.2〜1.3 であり,一方支持力の安全率は Fs = 3 と大きく数値が違うことに疑問を感じたことのある人は多いのではないでしょうか。
ここでは,それぞれの安全率の違いと両者の関係についてまとめてみました。
両者の違いは,端的に言ってしまえば安全率の定義の違いです。(これじゃ分からん,という声が聞こえてきそう・・・)
斜面安定の安全率の定義は Fs = S/τ であり,せん断抵抗力とすべり力の比です。
この式は τ = S/Fs = (σtanφ+c)/Fs とも書けることから,安全率はせん断強度そのものの一次の低減係数であるともいえます。つまり,例えば Fs = 1.2 の斜面があったとき,この地盤の tanφ,c を1/1.2倍すれば,結果は単純に Fs = 1.0 となります。
一方,支持力の安全率の定義は Fs = qu/qa であり,地盤上に載せることができる極限荷重と載荷重との比です。
従って,安全率の意味が最初から全く違っています。
また極限支持力は qu = c*Nc + po*Nq + (γ/2)*B*Nγ と,それぞれの項に別々の支持力係数が掛かります。
これらの支持力係数はせん断抵抗角 φ に対して指数関数的に変化し,一般的な土の φ = 30° の付近では φ が数度増減するだけで,支持力係数は倍半分と大きく変化します。
従って支持力においては, φ=0 の場合を除いて,せん断強度 tanφ,c が1/2になっても,極限支持力は1/2とはなりません。(一般に1/2よりはるかに小さくなります。)
ここで注意しなければならないのは,支持力は地盤への載荷重として扱われるので,荷重が変われば当然地盤内部の応力状態も変化することです。
それでは,平坦な地盤に荷重を載荷した場合の斜面安定の安全率(せん断抵抗力とすべり力の比)と支持力の安全率(極限荷重と載荷重の比)の関係を考えてみます。
φ=0 の粘土地盤であれば話は簡単で,この場合,中心角 θ=66.8° の円弧すべり面を成すことが既に分かっています。
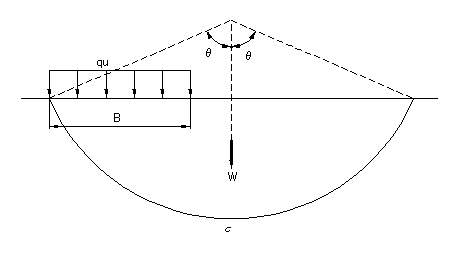
粘土地盤に載荷したときのすべり面
極限荷重qcを載荷すると,せん断抵抗力とすべり力の比で定義した安全率 Fss は当然1.0となります。(Fss : Safety Factor of Sliding)
平坦な地盤なため,土の自重によるすべり力はゼロとなるので,結局すべり力は荷重によるものだけとなり,荷重を qa = qu/Fsb まで小さくすると,すべり力 τ も極限荷重 qu を載荷したときの1/3となります。(Fsb : Safty Factor of Bearing)
一方, φ=0 なので,せん断抵抗力 S は,地盤内の応力の変化とは関係なく c*L で一定です。
従って τ → 1/3 , S = const なので, Fss = S/τ = 3.0 となり, Fsb = 3 と一致します。
(但し粘土地盤であっても,長期の支持力問題であれば排水条件下のせん断となります。)
砂地盤の場合,話はかなり難しくなります。
すべり面は,せん断抵抗角に応じた対数ら線を成します。また,せん断抵抗力 σtanφ が地盤内の応力に依存することから,スケールと土の密度が無視できなくなります。
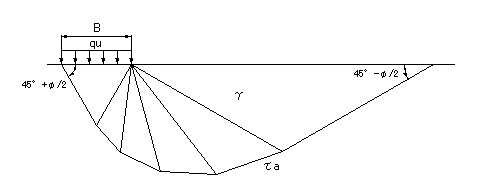
砂地盤に載荷したときのすべり面
c=0 の砂地盤において,荷重を qu → qa に低減したとき,すべり力は1/3になりますが, φ≠0 なので荷重の低減に伴いせん断抵抗力も小さくなり S は極限荷重を載荷したときより小さくなります。
従って τ → 1/3 , S → 元の値より小,なので,安全率 Fss は極限荷重を載荷したときの1.0よりは大きくなりますが,一般に3.0よりはかなり小さな値となります。
(かなりってどれくらい?)
どれだけ小さくなるかは,せん断抵抗角,基礎幅,土の密度によって変わるため一概には言えませんが,組み合わせによっては斜面の安全率と同レベル程度まで小さくなる可能性があります。
ただしこれを計算しようとすると,すべり面が複雑な非円弧であり,すべり土塊間に働く内力が無視できないので, Janbu 法などの力の釣り合いにより厳密な方法を用いて qu → min となる対数ら線の極を探す必要があり,かなり面倒です。
(このため,きちんとした計算はしていません。概算では φ=30°,B=2.0m,ρ=2000kg/m^3 で q=qu/3 のとき, Fss=1.4 程度という結果を得ましたが,精度に自信はありません。)
(追記 : 上の計算は実は個別要素法によるもので,このとき極限荷重から支持力係数を逆算すると Nγ = 18.7 を得ました。
Terzaghi によると φ=30°のときの近似値は Nγ ≒ (Nq-1)tan(1.4φ) = 19.3 なので,細かな部分を詰めていない概略計算結果としては良い線ではないでしょうか。一方,同じ土性値,すべり面形状により Janbu 法で解くと, Nγ = 21.4 , q=qu/3 のとき Fss=1.66 となりました。いずれの計算でも簡便のために対数ら線の極は荷重端部に固定しています。
また,円弧すべり面を仮定して Bishop 法で解くと, Nγ = 37 , q=qu/3 のとき Fss=1.32 となりました。もう少し真面目に検討して整理すると,面白い結果がでるかもしれません。2003.8.27 )
いずれにせよ,斜面安定の安全率と,支持力の安全率とは全然意味が違っており,両者の関係はせん断強度 tanφ,c や基礎幅,土の密度によって変わるため,一概に”とっちがどっち”とは言えないということです。
次に斜面上の支持力について考えてみます。
少し意地悪なケースなので,ちょっと考えてみて下さい。
ある所に,何も載荷されていない状態の斜面が在り,この斜面の”斜面安定に関する”安全率が Fss = 1.5 であったとします。
次に,斜面上に荷重 qu を載荷したとき,斜面が極限状態の安全率 Fss = 1.0 となったので,この qu を”極限支持力”と考えて,この荷重を”支持力に関する”安全率 Fsb = 3 で割った値 qa = qu/Fs を許容支持力としました。
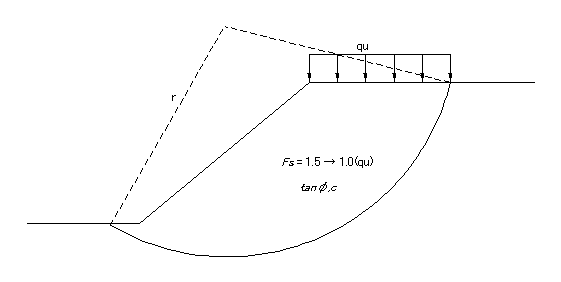
斜面上に載荷したときのすべり面
一応の理屈は通っていますよね? 確かに qu を載荷したときに,斜面全体の力の釣り合いは極限状態になっているし,その荷重を安全率 Fsb = 3 で除した値を許容支持力として定義しているし。
でも,本当にこれで良いのでしょうか?
次に,荷重 qa を載荷したときの斜面の安全率 Fss を考えてみます,このケースでは少なくとも Fss = 1.5〜1.0 の間にあることは確かです。比率からすると,おそらく Fss = 1.3 前後ってトコでしょうか。
これであれば,どちらも許容安全率を満足しているので OK とかなりそうですね?
しかし問題は,この考え方に基づくと Fss > 1.0 でさえあれば,どれほど元の斜面安定に対する安全率が小さくても,立派に支持力に対する安全率 Fsb = 3 を満足した許容支持力 qa が定義できてしまうことです。
現実問題として,いくら極限荷重に対する安全率 Fsb = 3 といっても,斜面安定に対する安全率 Fss = 1.1 であったら,誰も安全であるとは判断しません。
このような場合は,斜面安定に対する安全率,例えば Fss = 1.3 を満足する載荷重を許容支持力として評価すべきだと思います。
また,ここで Fss と Fsb を混同してしまうと,斜面安定計算をしているのにも関わらず安全率 Fs = 3 が必要,なんて不思議な事態に陥ってしまいます。(岩盤でもない限り,一般的な土のせん断強度と斜面勾配で安全率 Fs = 3 なんて滅多にお目にかからないと思います。)
なお,「港湾の施設の技術上の基準・同解説」では,ケーソン基礎の捨石マウンドの支持力の照査として,Bishop法による円弧すべり法を用いた方法を紹介しています。
円弧すべり法によって地盤の支持力を評価する場合の参考になるのではないでしょうか。
出典及び関連文献
(社)日本港湾協会 :「港湾の施設の技術上の基準・同解説」


