本来，斜面安定は一つの現象なので，安全率も正解値は一つのはずです。

しかし，極限平衡法による斜面安定の計算には，非常に多くの式が提案されています。
ここでは，力の釣り合いの観点から，極限平衡法による斜面安定についてまとめてみました。

---

それにしても，式の数が多いと思いませんか？　あるソフトハウスが販売している斜面安定計算プログラムが対応している設計基準を数えてみたら，円弧すべりが15，複合すべりが6の合計21式にもなりました。

実際には，発注機関ごとの”設計基準式”となるので，違う設計基準式でも中身は同じ式といえるものが多くあります。
そのような”提案式”の代表的なものとして，円弧すべりでは Fellenius 法，修正 Fellenius 法， Bishop 法， Spencer 法，複合すべりでは janbu 法， Morgenstern & Price 法，などがあり，他にもいろいろあるようです。

何故これほど多くの式があるのか。
これは，極限平衡法では”正解”を得るのが難しいことが理由だと思われます。

---

ご存知の方も多いと思いますが，極限平衡法による斜面安定の計算は高次の不静定問題です。

すべり土塊をｎ個のブロックに分割します。
各ブロックに働く力は，すべり面上の垂直力 Ｎi ，せん断力 Ｔi ，ブロック間に働く垂直力 Ｅi ，せん断力 Ｘi です。また， Ｅi の作用高さを ｈi とします。

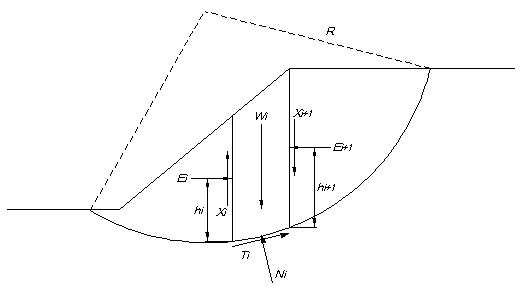
この時の未知数は， Ｎi がｎ個， Ｅi ， Ｘi ， ｈi がそれぞれｎ−1個，それに安全率 Ｆs が1個なので，合計すると4ｎ−2個となります。（ここで， Ｔi は， Ｆs の関数として求めます。）

一方，各ブロックごとの水平，垂直，モーメントの釣り合いより，3ｎ個の関係式が得られます。
従って，結局ｎ-2個の未知数が余分な不静定問題となり，このままでは解くことはできません。
このため，解を求めるためには何らかの形で問題を静定化する必要があります。

多くの式が提案されている理由はここで，問題の静定化のための仮定の数だけ式があるといえます。
そして，当然仮定が違えば，出てくる安全率にも違いが生じます。式によっては特有のクセのような現象が発生します。

---

現在最も広く用いられているのは，おそらく Fellenius 法，修正 Fellenius 法の系統で，多くの設計基準式がこれに属しています。

これも良く知られていることですが， Fellenius 法は，力の釣り合いのうちモーメントの釣り合いしか満たしていません。つまりブロック間に働く内力 Ｅi ， Ｘi を無視しており，力の釣り合いの点からはかなり大胆な方法といえます。

Ｆs ＝ Σ（ｃ*Ｌ ＋ Ｗ*cosα*tanφ）／Σ（Ｗ*sinα）
 

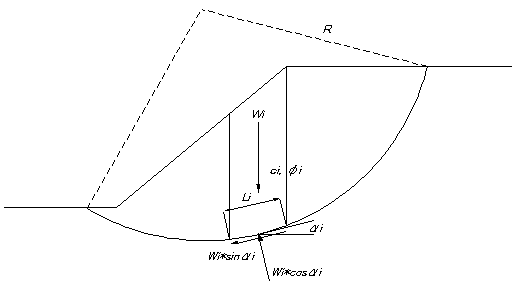
また Fellenius 法は，間隙水圧が大きいほど，すべり面の円弧の中心角が大きいほど誤差が大きくなることが指摘されています。
一度 Fellenius 法で水没斜面の安全率を計算してみて下さい。 Bishop 法などと比較すると，土性値，水位および斜面形状にもよりますが，安全率で0.1〜0.2，あるいはそれ以上小さな結果を示す場合があります。
元々，計画安全率 Fsp = 1.2〜1.3 程度の斜面安定の検討で，この誤差は決して小さくはないですよね？

このような計算式が広く使われている理由として，(1)計算が簡単で手計算可能，(2)誤差が安全側である，とかなり昔からいわれ続けています。

しかし，(2)はともかくとして，これだけパソコンが高性能化し，普及した今となっては(1)は理由となるのでしょうか？

---

個人的な感想になってしまいますが．．．

せっかく現地で一所懸命に断面形状を測量して，丁寧に土質試験をして地盤の構成や土性値を求めているのに，肝心の安全率の計算の場面だけ”結果が安全側だからいいじゃない”といってしまうのは，個人的には何かバランスの悪さを感じます。

一方で，元々斜面安定の検討には様々なファクターで多くのプラスマイナスの誤差を含んでいるのだから，計算式だけ厳密にすることにどれだけの意味があるのか？　という反論を受けることもあります。確かにこの意見にも一理あると思います。

地盤工学の永遠のテーマであり，古くて新しい問題である”斜面安定”。
みなさんはどう感じておられるのでしょうか？