おぼえがき

安全率，力の釣り合い，と内容的にはどんどん遡っている感がありますが，斜面安定ネタが続きます。
今回は，さらに遡って極限平衡法による斜面安定における内力についての話題です。

力の釣り合いのところでも述べていますが，極限平衡法による斜面安定は高次の不静定問題なので，すべり土塊間に働く内力の作用位置，方向，大きさすべてを正確に求めることは結構難しいのです。

従って多くの場合，内力の作用位置や方向に何らかの仮定を設けています。

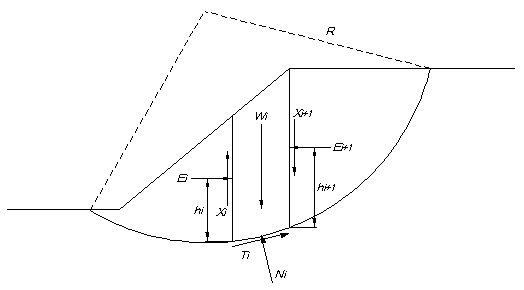
ここで，各ブロック間に働く垂直力Ｅi ，せん断力Ｘi ，またＥi の作用高さをｈi とします。

それでは，内力は実際にはどのように働いているのか少し考えてみます。

まず，地表面に載荷重などが作用していない水平な地盤を考えてみます。
この時，深度方向の土圧の分布は三角形なので，ブロック間に働く垂直力Ｅi の合力の作用高さｈi は下端から1/3の位置となります。
地表面の土圧がゼロであることから当たり前のことではあるのですが，下端から1/3の作用高さとは断面の核の縁にあることを意味しています。もし合力の作用高さがこれより低い位置であれば，地表面には引張力が発生することになります。

また，このケースでは，ブロック間相互に上下方向の力は働かないので，ブロック間に働くせん断力Ｘi はゼロとなります。
従って，Ｅi の大きさは静止土圧の合力，作用高さｈi は下端から1/3となり，Ｘi はゼロとなります。

次に，これが斜面ではどうなるのでしょう。

単純に言ってしまえば，Ｅi の大きさ，ｈi の高さは水平地盤の場合とは異なり，Ｘi もゼロではなくなります。
具体的にはどう変わるかというと，実は結構難しい問題だったりします。例えばある本では，”作用高さは1/3あるいはこれよりやや高い位置”と記載されています。
感覚的には概ね1/3から1/2の範囲ではないかと思うのですが，”やや高い位置”といわれても正直困ってしまいませんか？

下図のような形状，物性値を持つモデル地盤で計算してみました。

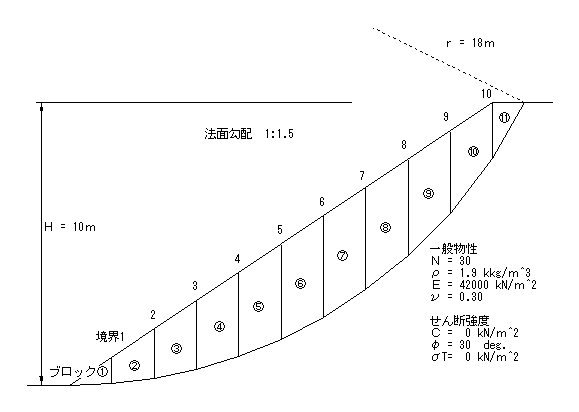
Janbu 法により，作用高さ ｈi = Ｈi/3 と仮定したときの，各ブロック境界に働く内力の計算結果は以下の通りです。この時の斜面全体の安全率は Ｆs = 1.07 で，また内力が安全率へ与える影響は，起動力で約-10％，抵抗力で約-3％となりました。
従って内力を考慮すると，起動力の低減の効果が相対的に大きいため，無視した場合よりも安全率は大きな値を示します。

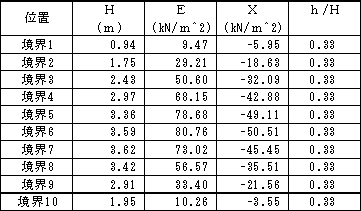
作用高さ ｈi = Ｈi/3 より土圧は三角形分布となるので，これを土圧係数ｋとして逆算すると斜面上部の境界10ではｋ = 0.28，中央部の境界5では0.73，下部の境界1では1.13となります。数値としては，かなり大きな値であると思いませんか？

また，斜面の上部と下部とでこれだけ土圧の作用状況が違っているのに，本当に ｈi/Ｈi = const と仮定してよいのか，個人的には不思議に感じます。

そこで内力の大きさと作用高さを同時に求めるために，例によって個別要素法を用いて同じモデル地盤で内力を計算した結果は以下の通りです。この時の斜面全体の安全率は Ｆs = 1.05 となりました。

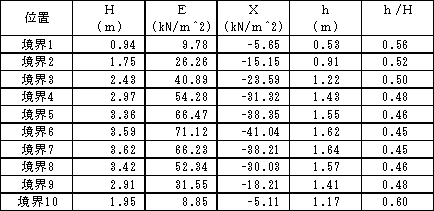
この条件では，斜面全体の安全率および内力の大きさは両者とも比較的良く一致しているのですが，個別要素法では内力の作用高さが ｈ/Ｈ = 0.45～0.60 とかなり高い位置を示しています。従って，当然土圧は台形分布を示しています。

このモデルでは，すべり土塊を水平方向のみ分割しているため，特に斜面中央部のブロックは非常に縦長の形状をしています。
実際の地盤ではともかく，このような形状に分割した剛体ブロック相互の運動としては，それほどおかしな値ではないと思うのですが，どうでしょう？
このため，ブロック分割を有限要素法のように水平方向，鉛直方向とも細かく分割すると，もっと実地盤に近い挙動を示すかもしれません。（機会があれば細かくブロック分割したモデルで解析して，その結果を公表したいと思います。）

先の Janbu 法の計算結果からも，内力の寄与率はたかだか全体の数％程度のオーダーです。
無視した方が安全側ということもあり，どちらかといえばあまり重要視されて来なかったと思います。

しかし個人的には，斜面内の局所的な安全率や内力の分布，さらに進行性破壊などは非常に興味のある分野です。

また，このように細かな技術論とは別の話になりますが，一つはコスト縮減，もう一つは説明責任などの点から，単純に”安全側だからＯＫ”という論理はいずれ通用しない時代が来るのではないかと考えています。